Intro to Survival Analysis
2025-04-20
Introduction to Survival Analysis
In this module, we’ll explore how to model time-to-event data using R. You’ll learn how to analyze and visualize a variety of methods to understand survival patterns — even when we don’t have the complete data for every individual.
Objectives
The objective of this module is to provide an applied introduction to survival analysis using R. To complete this module, prior familiarity with R syntax and basic statistical concepts such as regression and probability, is expected.
What is Survival Analysis?
Imagine you’re tracking patients in a clinical trial to see how long it takes for them to recover. Not all patients finish the study, and some will never experience the event (recovery) — that’s where survival analysis comes in!
Key Idea: Time-to-Event Data In survival analysis, we care not only about what happens, but when it happens.
There are two ways to think about time in this framework:
- Points: The exact time an event occurs (e.g., someone
relapses, dies, or gets a job)
- Lines: The duration from the start of observation
until the event. This could be days, months, or even years.
This structure makes survival analysis unique from other statistical models. It is built to handle incomplete information and uncertain timing.
Key Concepts
- Time to event: How long it takes until something
happens
- Censoring: When the event is not observed, but the
data is still usable
- Survival function: Probability of surviving past
time t
- Hazard function: Instantaneous risk of the event
occurring at time t
- Hazard ratio: Compares the risk between two groups (e.g., treated vs control)
Types of Censoring
Survival analysis handles incomplete data using the concept of
censoring:
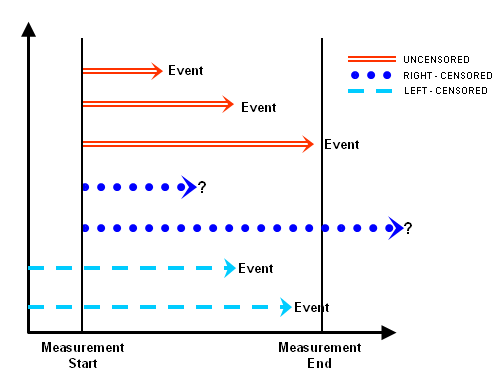
- Right censoring (most common): The event hasn’t
happened yet, and we don’t know when (e.g., someone is still alive at
study’s end)
- Left censoring: The event has already occurred
before observation started
- Interval censoring: The event happened between two known time points
A Bit of History
Survival analysis has deep historical roots. In 1662, John Graunt created one of the first life tables by analyzing London’s death records. His goal was to understand the patterns of mortality and lifespan — essentially starting the earliest form of population-based survival analysis.
For centuries, survival analysis was primarily used to study death and mortality rates, especially in public health. In the last few decades, this method has grown beyond medicine.
Core Functions
Survival Function \(S(t) = P(T > t)\):
Represents the probability that an event has not occurred by time tHazard Function \(h(t)\):
Represents the instantaneous rate at which the event occurs at time t, given that the individual has survived up to that time
> “If someone has made it to time t, how likely are they to experience the event right now?”Hazard Ratio
\[HR = \frac{\text{Hazard when } x = 1}{\text{Hazard when } x = 0}\]
Compares the risk between two groups
> Example: An HR = 2 means one group is twice as likely to experience the event at a given moment than another group.
Why Not Traditional Models?
- Every individual has a known outcome
- No one drops out
- The timing of events isn’t important
But in the real world:
- Not everyone reaches the event
- People drop out
- Timing matters
Survival analysis is designed for real-world situations!
Useful Skills You’ll Learn Today
We will apply survival analysis techniques to five challenges using
data from the survival package in R, including:
- Kaplan-Meier Estimation
- Cox Proportional Hazards Model
- Time-Varying Covariates
- Group comparison
- Visualizing Competing Risks with CRR
Using R for survival analysis
In this module, we’ll be applying survival techniques using R. We’ll focus on key functions such as:
survfit(): Estmates survival functions and generates Kaplan-Meier curves.
coxph(): Fits the Cox proportional hazards model to analyze the effects of covariates on survival
These functions allow us to analyze time-to-event data and assess the effects of different variables on survival outcomes.
Let’s begin:
Challenge 1
Fitting the Kaplan-Meier Survival Model
The Kaplan–Meier estimator, also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss, the time-to-failure of machine parts, or in our case, the amount of time a patient survived after being diagnosed for a disease.
For this challenge, we will start with a basic dataset of twelve Colon cancer patients in a study who have survived after diagnosis.
We will now read the dataset (Csurv) which I prepared specially for this challenge:
library(readxl)
github_url <- "https://raw.githubusercontent.com/imcarlyy/survival_analysis/main/Csurv.xlsx"
temp_file <- tempfile(fileext = ".xlsx") # Create a temporary file
download.file(github_url, temp_file, mode = "wb") # 'wb' for binary (Excel files)
Csurv <- read_excel(temp_file) # Read the downloaded file
unlink(temp_file) # Delete the temporary fileNow I will check the names of the variables given in this table.
## [1] "Time" "Death"## # A tibble: 12 × 2
## Time Death
## <dbl> <dbl>
## 1 2 1
## 2 3 0
## 3 6 1
## 4 6 1
## 5 7 1
## 6 10 0
## 7 15 1
## 8 15 1
## 9 16 1
## 10 27 1
## 11 30 1
## 12 32 1It is very important to know while working with survival analysis datasets what the 0 and 1 stands for.
In this example we are considering Death: 1=event has occurred (death) and 0=no event (they are censored; meaning they have left the study and hence we do not know whether they have data on them at the given point of time).
So, in this dataset if we look at first column, the 1st individual died at 2 months from the start of the study (Time=2, Death=1), the 2nd individual was censored at 3 months (Time=3, Death=0), the 3rd individual died at 6 months (Time=6, Death=1) and so on.
Now we will look into the Kaplan-Meier to fit into this dataset.
In order to do this, we need to load the survival library into R. Now, the survival library is already built into base R, so we do not need to install this package, but we do need to load the package to use these survival commands.
Now in order the fit the K-M model, we will use this survfit command and so I am going to fit a survival analysis, store it in an object called km.model:
Here, I am going to let R know the type is kaplan-meier (if we do not specify the type it will fit the kaplan-meier by default so it wouldn’t have been an issue)
Now the way we specify the survival time or the y variable is using a capital S; so it’s Surv (survival) and then in parentheses we need to give it both the time the individual was followed for as well the indicator of whether the event occured (they died) or if they were censored {Surv(Time, Death) tilde 1} and the reason we have one here is that for this dataset we don’t actually have any x variables. This is the way we let R know that we are just estimating survival without using any particular X variables.
Now that the model has been fit, we can ask a few summaries…
## Call: survfit(formula = Surv(Time, Death) ~ 1, type = "kaplan-meier")
##
## n events median 0.95LCL 0.95UCL
## [1,] 12 10 15 7 NAThe output we are getting here is the total number of individuals is 12, number of events is 10 (10 deaths and 2 censored observations), median survival time so, in this case half the people survived beyond 15 months, half did not. We have also returned a 95% confidence interval for the median which means that we are 95% confident that median survival is somewhere between 7 months and infinity. This dataset is very small so here we do not have a upper limit for confidence interval around the median survival.
We can also ask for the summary of the model:
## Call: survfit(formula = Surv(Time, Death) ~ 1, type = "kaplan-meier")
##
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 2 12 1 0.917 0.0798 0.7729 1.000
## 6 10 2 0.733 0.1324 0.5148 1.000
## 7 8 1 0.642 0.1441 0.4132 0.996
## 15 6 2 0.428 0.1565 0.2089 0.876
## 16 4 1 0.321 0.1495 0.1287 0.800
## 27 3 1 0.214 0.1325 0.0635 0.720
## 30 2 1 0.107 0.1005 0.0169 0.675
## 32 1 1 0.000 NaN NA NAHere we can see that at time 2, there were 12 individuals at risk, 1 death occurred, the probability of surviving beyond 2 months is 91.7%. We also have a standard error associated with that survival (0.0798) as well as a 95% CI (ie. we are 95% confident that beyond 2 months the patients survival chances are between 77.3% upto a 100%). Similary, at time 6, there are 10 individuals at risk, 2 individuals died and so the probabilty of surviving beyond 6 months is 73.3%. Again, the standard error at 6 months is 0.1324 and we are 95% confident that there’s somewhere between 51.5 upto 100% chance of surviving 6 months. Now these are extremely wide confidence intervals because the sample size is so small. This dataset is useful for introducing the idea of Kaplan-Meier survival model but for a real study, we would have a same size of much greater than 12.
Now we can ask R to make a plot of this model. To do that we can ask R to plot the K-M model. So R will plot the Kaplan-Meier model that was fit saying confidence interval=F (or False). It tells R to not put a confidence interval around the survival function. xlab and ylab are giving the plot x-axis and y-axis labels and the main is the title.
As we can see, a plot of the Kaplan–Meier is a series of declining horizontal steps.
Now if we wanted to we can ask R to put confidence interval or confidence bands around this survival function. To do so we would just set conf.int=T (or True). I will also set las=1 (this will rotate the values on the y-axis. So, here’s what it will look like:
We can see now these dashed lines give us confidence interval around the survival function and we can also see that las = 1 argument rotated the values on y-axis.
Now I am going to add a red horizontal line at S(t) = 50% into this plot:
plot(km.model, conf.int=T, xlab="Time (months)", ylab="%Alive = S(t)", main="K-M Model", las=1)
abline(h=0.5, col="red")The red line is at 50% meaning 50% surviving 50% not. Hence, this is how we look at the median survival. Here the red line crosses the survival function right at the 15 months (this is our median). The red line passes the dashed line for lower limit at 7 months and it never hits the dashed line for upper limit (because of the smaller sample size).
Now, I am going to produce the same plot again but added mark.time=TRUE and this will add in little tick marks wherever there was a censored observation. So if you remember there was observations censored at 3 and at 10 months. So, here’s the code:
plot(km.model, conf.int=T, xlab="Time (months)", ylab="%Alive = S(t)", main="K-M Model", las=1, mark.time=TRUE)This helps us visualize where and when observations are censored.
Now, let’s include a x variable into fitting this model. I will continue on the same cancer patient dataset (those 12 individuals were all under 40 years old) and will add in more data points and this is going to be a group of individuals who are over 40 years old (another column Over40 will be added)
rm(Csurv)
library(readxl)
github_url2 <- "https://raw.githubusercontent.com/imcarlyy/survival_analysis/main/Csurv40.xlsx"
temp_file2 <- tempfile(fileext = ".xlsx") # Creates a temporary file path
download.file(github_url2, temp_file2, mode = "wb") # Saves to temp_file2 (not temp_file)
Csurv40 <- read_excel(temp_file2) # Reads from temp_file2
unlink(temp_file2) # Deletes temp_file2Taking a quick look at the new table:
## # A tibble: 6 × 3
## Time Death Over40
## <dbl> <dbl> <dbl>
## 1 2 1 0
## 2 3 0 0
## 3 6 1 0
## 4 6 1 0
## 5 7 1 0
## 6 10 0 0## # A tibble: 6 × 3
## Time Death Over40
## <dbl> <dbl> <dbl>
## 1 1 1 1
## 2 2 1 1
## 3 3 1 1
## 4 3 1 1
## 5 9 1 1
## 6 22 0 1Over40=0 : not over 40 years old; Over40=1: Over 40 years old
Now let’s fit the K-M Model (say km.model2), relating over/under40 to survival and see if there is a relationship between survival and age:
Plotting this:
plot(km.model2, conf.int=F, xlab="Time (months)", ylab="%Alive = S(t)", main="K-M Model", data=Csurv40) #conf.int=F, so we will not put the confidence bands on there for now.## Warning in plot.window(...): "data" is not a graphical parameter## Warning in plot.xy(xy, type, ...): "data" is not a graphical parameter## Warning in axis(side = side, at = at, labels = labels, ...): "data" is not a
## graphical parameter
## Warning in axis(side = side, at = at, labels = labels, ...): "data" is not a
## graphical parameter## Warning in box(...): "data" is not a graphical parameter## Warning in title(...): "data" is not a graphical parameterAs we can see, we clearly see a difference between under 40 and over 40 groups: Under 40 groups have a higher chance of survival than over 40 groups.
Let’s do some summaries:
## Call: survfit(formula = Surv(Time, Death) ~ Over40, data = Csurv40,
## type = "kaplan-meier")
##
## Over40=0
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 2 12 1 0.917 0.0798 0.7729 1.000
## 6 10 2 0.733 0.1324 0.5148 1.000
## 7 8 1 0.642 0.1441 0.4132 0.996
## 15 6 2 0.428 0.1565 0.2089 0.876
## 16 4 1 0.321 0.1495 0.1287 0.800
## 27 3 1 0.214 0.1325 0.0635 0.720
## 30 2 1 0.107 0.1005 0.0169 0.675
## 32 1 1 0.000 NaN NA NA
##
## Over40=1
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 9 3 0.667 0.157 0.4200 1.000
## 2 5 1 0.533 0.173 0.2821 1.000
## 3 4 2 0.267 0.159 0.0829 0.858
## 9 2 1 0.133 0.123 0.0218 0.817## Call: survfit(formula = Surv(Time, Death) ~ Over40, data = Csurv40,
## type = "kaplan-meier")
##
## n events median 0.95LCL 0.95UCL
## Over40=0 12 10 15 7 NA
## Over40=1 9 7 3 1 NANow, let’s make that same plot again but adding some colours, a legend and a tick at the time of censored events:
plot(km.model2, conf.int=F, xlab="Time (months)", ylab="%Alive = S(t)", main="K-M Model", col=c("red","blue"), las=1, lwd=2, mark.time=TRUE, data=Csurv40 )## Warning in plot.window(...): "data" is not a graphical parameter## Warning in plot.xy(xy, type, ...): "data" is not a graphical parameter## Warning in axis(side = side, at = at, labels = labels, ...): "data" is not a
## graphical parameter
## Warning in axis(side = side, at = at, labels = labels, ...): "data" is not a
## graphical parameter## Warning in box(...): "data" is not a graphical parameter## Warning in title(...): "data" is not a graphical parameterlegend(18, 0.95, legend=c("Under 40 years", "Over 40 years"), lty=1, lwd=2, col=c("red", "blue"), bty="",cex=0.6) #adding a legendAn important question:
Are two survival functions are statistically significantly different? Or do you think that the survival differs if someone is over or under 40?
YES! Survival (Probability of surviving beyond a certain time) changes depending on if someone’s over or under 40. Here I will talk about the formal test for doing this.
Here comes the Log-Rank Test: It is a way of testing if there is a significant difference between the two survival curve. It is also known as the Mantle Hansel test.
#Log-Rank Test
#Null Hypothesis: Survival for two groups is same
#Hypothesis1: Survival for two groups is not same
survdiff(Surv(Time, Death)~Over40, data=Csurv40)## Call:
## survdiff(formula = Surv(Time, Death) ~ Over40, data = Csurv40)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## Over40=0 12 10 13.35 0.841 4.75
## Over40=1 9 7 3.65 3.079 4.75
##
## Chisq= 4.8 on 1 degrees of freedom, p= 0.03Test-statistic is 4.8, the p-value is 0.03. Based on this small p-value, we can reject our null hypothesis. We have evidence to believe that survival is not the same depending on if you are over or under 40.
Challenge 2:
Cox proportional hazard model: Checking the proportional hazards assumption
## Loading required package: ggplot2## Loading required package: ggpubr##
## Attaching package: 'survminer'## The following object is masked from 'package:survival':
##
## myeloma##
## Attaching package: 'dplyr'## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionLet’s say you want to assess the role of different variables in your data in survival times. There are many models and methods to do so but the most common is to use the Cox Proportional Hazard model. First introduced in 1972, this model allows you to assess the hazard at a certain time given a specific covariate. In math terms, under the cox model our hazard function is:
 Where the hazard at time t
given your covariate X is equal to your baseline hazard function (with
all covariates equal to 0), multiplied by your exponential function
exp(BX), a multiplicative way of assessing the covariates influence on
overall hazard.
Where the hazard at time t
given your covariate X is equal to your baseline hazard function (with
all covariates equal to 0), multiplied by your exponential function
exp(BX), a multiplicative way of assessing the covariates influence on
overall hazard.
Let’s load in our datasets.
As before we’ll make a survival object based on some of our data. In this case let’s use the lung cancer survival dataset:
The Survival package makes fitting a CPH model to your data very easy, with just the coxph function. Say we wanted to fit a Cox regression based on age to our cancer mortality data:
## Call:
## coxph(formula = Surv(time, status) ~ age, data = lung)
##
## coef exp(coef) se(coef) z p
## age 0.018720 1.018897 0.009199 2.035 0.0419
##
## Likelihood ratio test=4.24 on 1 df, p=0.03946
## n= 228, number of events= 165However, the CPH model makes some assumptions!
The covariates that you’re testing are constant over time.
Hazard ratios/proportions do not vary over time.
The second one is the most important. Put simply it means that the proportion of hazard between groups in your model is the same at every time point. This is referred to as the “proportional hazards assumption” and is the reason it’s called the Cox Proportional Hazard model. This limits the model’s utility, and means that we need to test to see if our data can be used with the cox model. Luckily the survival package makes this pretty straightforward using the cox.zph() function:
## chisq df p
## age 0.346 1 0.56
## GLOBAL 0.346 1 0.56The function returns a p value of 0.56, which is far above even our least stringent alpha levels so we can be pretty confident that our age data does not violate the proportional hazard assumption. Hooray!
Let’s have a look at our cox model based on age again:
## Call:
## coxph(formula = Surv(time, status) ~ age, data = lung)
##
## coef exp(coef) se(coef) z p
## age 0.018720 1.018897 0.009199 2.035 0.0419
##
## Likelihood ratio test=4.24 on 1 df, p=0.03946
## n= 228, number of events= 165The coefficient is positive, so we’re seeing a slight increase in the risk of an “event” (in this case death) due to age, with a significant p-value of 0.0419. Though note that this p-value is on the higher end, so we might want to take this result with a grain of salt.
Try it on your own!
Fit a CPH model to the cancer data, looking at sex in addition to age. Does our model using sex violate the proportional hazard assumption? How does it’s p-value compare to that of age? What might account for this?
## chisq df p
## sex 2.608 1 0.11
## age 0.209 1 0.65
## GLOBAL 2.771 2 0.25## Call:
## coxph(formula = Surv(time, status) ~ sex + age, data = lung)
##
## coef exp(coef) se(coef) z p
## sex -0.513219 0.598566 0.167458 -3.065 0.00218
## age 0.017045 1.017191 0.009223 1.848 0.06459
##
## Likelihood ratio test=14.12 on 2 df, p=0.0008574
## n= 228, number of events= 165Curiously, sex is showing a strong negative coefficient, indicating that it’s having a strong protective effect (i.e. females are surviving longer than males in this dataset), and our p-value for that is 0.002, which is significant by most metrics! That said, if we look at the cox proportional hazard assumption test our p-value associated with sex is pretty low, at 0.11. This is a little concerning, since while we’re still technically above an alpha threshold of 0.05, we might be concerned that our sex covariate is violating the proportional hazard assumption. What do our survival curves look like?
plot_1 <- ggsurvplot(
survfit(Surv(time, status) ~ sex, data = lung),
legend.labs = c("Male", "Female"),
palette = c("purple","forestgreen"),
conf.int = T
)
plot_1Hmm, our survival plots seem to be drawing together towards the end of the timeframe we’re looking at. Perhaps that accounts for the low p-value in our proportional hazard test. What happens if we remove the individuals near the ends of the curves?
lung_short <- lung %>%
filter(
time < 700
) %>%
filter(
time > 50
)
cx_sex2 <- coxph(Surv(time, status) ~ sex + age, data = lung_short)
cox.zph(cx_sex2)## chisq df p
## sex 0.575 1 0.45
## age 0.500 1 0.48
## GLOBAL 1.112 2 0.57ggsurvplot(
survfit(Surv(time, status) ~ sex, data = lung_short),
legend.labs = c("Male", "Female"),
palette = c("purple","forestgreen"),
conf.int = T
)Ahh, interesting! If we omit the mortality events that occurred very early and very late in our time series data, the proportional hazard due to our sex variable becomes a lot more constant. Interestingly doing this also seems to drop our age p-value, but both are now far above what we would consider a significant violation of the proportional hazard assumption.
Challenge 3:
Now let’s try what we’ve learned with some other data sets. Have a look at the colon dataset provided by the survival package. This is a survival dataset for patients with colon cancer in a chemotherapy treatment trial, with the “rx” column indicating what treatment the patients received (either “Obs” for observation only, “rxLev” for treatment with just levamisole, or “rxLev + 5FU” for levamisole & the chemotherapy agent 5-FU). Does the rx covariate violate the proportional hazard assumption? What do the survival curves look like for this data when we segregate based on treatment? Does the chemotherapy seem to work?
## id study rx sex age obstruct perfor adhere nodes status differ extent
## 1 1 1 Lev+5FU 1 43 0 0 0 5 1 2 3
## 2 1 1 Lev+5FU 1 43 0 0 0 5 1 2 3
## 3 2 1 Lev+5FU 1 63 0 0 0 1 0 2 3
## 4 2 1 Lev+5FU 1 63 0 0 0 1 0 2 3
## 5 3 1 Obs 0 71 0 0 1 7 1 2 2
## 6 3 1 Obs 0 71 0 0 1 7 1 2 2
## surg node4 time etype
## 1 0 1 1521 2
## 2 0 1 968 1
## 3 0 0 3087 2
## 4 0 0 3087 1
## 5 0 1 963 2
## 6 0 1 542 1## chisq df p
## rx 0.648 2 0.72
## GLOBAL 0.648 2 0.72## Call:
## coxph(formula = Surv(time, status) ~ rx, data = colon)
##
## coef exp(coef) se(coef) z p
## rxLev -0.02090 0.97932 0.07683 -0.272 0.786
## rxLev+5FU -0.44101 0.64339 0.08391 -5.256 1.47e-07
##
## Likelihood ratio test=35.23 on 2 df, p=2.233e-08
## n= 1858, number of events= 920ggsurvplot(
survfit(Surv(time, status) ~ rx, data = colon),
conf.int = T,
pval = T,
pval.method = T
)Challenge 4:
One of the most common test in survival analysis is a nonparametric test known as log-rank test, which compares survival curves under the assumption of proportional hazards. It tests whether there is a statistically significant difference in survival between groups over time.
\(H_0: S_1(t) = S_2(t) \text{ for all } t\)
\(H_A: S_1(t) \neq S_2(t) \text{ for some } t\)
The null hypothesis states that survival functions \(S_1(t)\) and \(S_2(t)\) for the two groups are equal at all time points \(t\), there is no difference in survival between groups over time. While the alternative hypothesis states that the survival functions are not equal at some time point \(t\), so there is a difference in survival between the two groups.
How the log-rank test works is that is compares the observed number of events (e.g., deaths) in each group to the expected number under the assumptions that all group have the same survival experience. So it sums the differences over the entire study period.
\(X^2 = \frac{(O_1 - E_1)^2}{V_1}\)
Where:
\(O_1\) is the observed number of events in group 1
\(E_1\) is the expected number of events in group 1
\(V_1\) is the variance of difference
This statistic follows the chi-squared distribution with 1 degree of freedom
In R, we will be using the survdiff() function from the
{survival} package to perform comparisons between two
groups.
Lets first compare survival times between males and females in the
Lung dataset to help us answer the question:
- Is there a statistically significant difference in survival times between males and females?
## inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
## 1 3 306 2 74 1 1 90 100 1175 NA
## 2 3 455 2 68 1 0 90 90 1225 15
## 3 3 1010 1 56 1 0 90 90 NA 15
## 4 5 210 2 57 1 1 90 60 1150 11
## 5 1 883 2 60 1 0 100 90 NA 0
## 6 12 1022 1 74 1 1 50 80 513 0Lets check if the survival curves follow the proportion hazard assumptions.
# Fit a Cox Proportional Hazards model
cox_m1 <- coxph(Surv(time, status) ~ sex, data = lung)
# Test proportional hazards assumption
cox_t1 <- cox.zph(cox_m1)
# View the results
cox_t1## chisq df p
## sex 2.86 1 0.091
## GLOBAL 2.86 1 0.091The p-value for sex is greater than 0.05, then there is no evidence that proportional hazards assumption is violated for sex. Then we can move forward to perform the log-rank test between males and females.
# Convert sex to a factor with appropriate labels
lung$sex <- factor(lung$sex, levels = c(1, 2), labels = c("Male", "Female"))
# Fit the Kaplan-Meier Survival Curves
fit1 <- survfit(Surv(time, status) ~ sex, data = lung)
# View the summary of the survival curves
summary(fit1)## Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
##
## sex=Male
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 11 138 3 0.9783 0.0124 0.9542 1.000
## 12 135 1 0.9710 0.0143 0.9434 0.999
## 13 134 2 0.9565 0.0174 0.9231 0.991
## 15 132 1 0.9493 0.0187 0.9134 0.987
## 26 131 1 0.9420 0.0199 0.9038 0.982
## 30 130 1 0.9348 0.0210 0.8945 0.977
## 31 129 1 0.9275 0.0221 0.8853 0.972
## 53 128 2 0.9130 0.0240 0.8672 0.961
## 54 126 1 0.9058 0.0249 0.8583 0.956
## 59 125 1 0.8986 0.0257 0.8496 0.950
## 60 124 1 0.8913 0.0265 0.8409 0.945
## 65 123 2 0.8768 0.0280 0.8237 0.933
## 71 121 1 0.8696 0.0287 0.8152 0.928
## 81 120 1 0.8623 0.0293 0.8067 0.922
## 88 119 2 0.8478 0.0306 0.7900 0.910
## 92 117 1 0.8406 0.0312 0.7817 0.904
## 93 116 1 0.8333 0.0317 0.7734 0.898
## 95 115 1 0.8261 0.0323 0.7652 0.892
## 105 114 1 0.8188 0.0328 0.7570 0.886
## 107 113 1 0.8116 0.0333 0.7489 0.880
## 110 112 1 0.8043 0.0338 0.7408 0.873
## 116 111 1 0.7971 0.0342 0.7328 0.867
## 118 110 1 0.7899 0.0347 0.7247 0.861
## 131 109 1 0.7826 0.0351 0.7167 0.855
## 132 108 2 0.7681 0.0359 0.7008 0.842
## 135 106 1 0.7609 0.0363 0.6929 0.835
## 142 105 1 0.7536 0.0367 0.6851 0.829
## 144 104 1 0.7464 0.0370 0.6772 0.823
## 147 103 1 0.7391 0.0374 0.6694 0.816
## 156 102 2 0.7246 0.0380 0.6538 0.803
## 163 100 3 0.7029 0.0389 0.6306 0.783
## 166 97 1 0.6957 0.0392 0.6230 0.777
## 170 96 1 0.6884 0.0394 0.6153 0.770
## 175 94 1 0.6811 0.0397 0.6076 0.763
## 176 93 1 0.6738 0.0399 0.5999 0.757
## 177 92 1 0.6664 0.0402 0.5922 0.750
## 179 91 2 0.6518 0.0406 0.5769 0.736
## 180 89 1 0.6445 0.0408 0.5693 0.730
## 181 88 2 0.6298 0.0412 0.5541 0.716
## 183 86 1 0.6225 0.0413 0.5466 0.709
## 189 83 1 0.6150 0.0415 0.5388 0.702
## 197 80 1 0.6073 0.0417 0.5309 0.695
## 202 78 1 0.5995 0.0419 0.5228 0.687
## 207 77 1 0.5917 0.0420 0.5148 0.680
## 210 76 1 0.5839 0.0422 0.5068 0.673
## 212 75 1 0.5762 0.0424 0.4988 0.665
## 218 74 1 0.5684 0.0425 0.4909 0.658
## 222 72 1 0.5605 0.0426 0.4829 0.651
## 223 70 1 0.5525 0.0428 0.4747 0.643
## 229 67 1 0.5442 0.0429 0.4663 0.635
## 230 66 1 0.5360 0.0431 0.4579 0.627
## 239 64 1 0.5276 0.0432 0.4494 0.619
## 246 63 1 0.5192 0.0433 0.4409 0.611
## 267 61 1 0.5107 0.0434 0.4323 0.603
## 269 60 1 0.5022 0.0435 0.4238 0.595
## 270 59 1 0.4937 0.0436 0.4152 0.587
## 283 57 1 0.4850 0.0437 0.4065 0.579
## 284 56 1 0.4764 0.0438 0.3979 0.570
## 285 54 1 0.4676 0.0438 0.3891 0.562
## 286 53 1 0.4587 0.0439 0.3803 0.553
## 288 52 1 0.4499 0.0439 0.3716 0.545
## 291 51 1 0.4411 0.0439 0.3629 0.536
## 301 48 1 0.4319 0.0440 0.3538 0.527
## 303 46 1 0.4225 0.0440 0.3445 0.518
## 306 44 1 0.4129 0.0440 0.3350 0.509
## 310 43 1 0.4033 0.0441 0.3256 0.500
## 320 42 1 0.3937 0.0440 0.3162 0.490
## 329 41 1 0.3841 0.0440 0.3069 0.481
## 337 40 1 0.3745 0.0439 0.2976 0.471
## 353 39 2 0.3553 0.0437 0.2791 0.452
## 363 37 1 0.3457 0.0436 0.2700 0.443
## 364 36 1 0.3361 0.0434 0.2609 0.433
## 371 35 1 0.3265 0.0432 0.2519 0.423
## 387 34 1 0.3169 0.0430 0.2429 0.413
## 390 33 1 0.3073 0.0428 0.2339 0.404
## 394 32 1 0.2977 0.0425 0.2250 0.394
## 428 29 1 0.2874 0.0423 0.2155 0.383
## 429 28 1 0.2771 0.0420 0.2060 0.373
## 442 27 1 0.2669 0.0417 0.1965 0.362
## 455 25 1 0.2562 0.0413 0.1868 0.351
## 457 24 1 0.2455 0.0410 0.1770 0.341
## 460 22 1 0.2344 0.0406 0.1669 0.329
## 477 21 1 0.2232 0.0402 0.1569 0.318
## 519 20 1 0.2121 0.0397 0.1469 0.306
## 524 19 1 0.2009 0.0391 0.1371 0.294
## 533 18 1 0.1897 0.0385 0.1275 0.282
## 558 17 1 0.1786 0.0378 0.1179 0.270
## 567 16 1 0.1674 0.0371 0.1085 0.258
## 574 15 1 0.1562 0.0362 0.0992 0.246
## 583 14 1 0.1451 0.0353 0.0900 0.234
## 613 13 1 0.1339 0.0343 0.0810 0.221
## 624 12 1 0.1228 0.0332 0.0722 0.209
## 643 11 1 0.1116 0.0320 0.0636 0.196
## 655 10 1 0.1004 0.0307 0.0552 0.183
## 689 9 1 0.0893 0.0293 0.0470 0.170
## 707 8 1 0.0781 0.0276 0.0390 0.156
## 791 7 1 0.0670 0.0259 0.0314 0.143
## 814 5 1 0.0536 0.0239 0.0223 0.128
## 883 3 1 0.0357 0.0216 0.0109 0.117
##
## sex=Female
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 5 90 1 0.9889 0.0110 0.9675 1.000
## 60 89 1 0.9778 0.0155 0.9478 1.000
## 61 88 1 0.9667 0.0189 0.9303 1.000
## 62 87 1 0.9556 0.0217 0.9139 0.999
## 79 86 1 0.9444 0.0241 0.8983 0.993
## 81 85 1 0.9333 0.0263 0.8832 0.986
## 95 83 1 0.9221 0.0283 0.8683 0.979
## 107 81 1 0.9107 0.0301 0.8535 0.972
## 122 80 1 0.8993 0.0318 0.8390 0.964
## 145 79 2 0.8766 0.0349 0.8108 0.948
## 153 77 1 0.8652 0.0362 0.7970 0.939
## 166 76 1 0.8538 0.0375 0.7834 0.931
## 167 75 1 0.8424 0.0387 0.7699 0.922
## 182 71 1 0.8305 0.0399 0.7559 0.913
## 186 70 1 0.8187 0.0411 0.7420 0.903
## 194 68 1 0.8066 0.0422 0.7280 0.894
## 199 67 1 0.7946 0.0432 0.7142 0.884
## 201 66 2 0.7705 0.0452 0.6869 0.864
## 208 62 1 0.7581 0.0461 0.6729 0.854
## 226 59 1 0.7452 0.0471 0.6584 0.843
## 239 57 1 0.7322 0.0480 0.6438 0.833
## 245 54 1 0.7186 0.0490 0.6287 0.821
## 268 51 1 0.7045 0.0501 0.6129 0.810
## 285 47 1 0.6895 0.0512 0.5962 0.798
## 293 45 1 0.6742 0.0523 0.5791 0.785
## 305 43 1 0.6585 0.0534 0.5618 0.772
## 310 42 1 0.6428 0.0544 0.5447 0.759
## 340 39 1 0.6264 0.0554 0.5267 0.745
## 345 38 1 0.6099 0.0563 0.5089 0.731
## 348 37 1 0.5934 0.0572 0.4913 0.717
## 350 36 1 0.5769 0.0579 0.4739 0.702
## 351 35 1 0.5604 0.0586 0.4566 0.688
## 361 33 1 0.5434 0.0592 0.4390 0.673
## 363 32 1 0.5265 0.0597 0.4215 0.658
## 371 30 1 0.5089 0.0603 0.4035 0.642
## 426 26 1 0.4893 0.0610 0.3832 0.625
## 433 25 1 0.4698 0.0617 0.3632 0.608
## 444 24 1 0.4502 0.0621 0.3435 0.590
## 450 23 1 0.4306 0.0624 0.3241 0.572
## 473 22 1 0.4110 0.0626 0.3050 0.554
## 520 19 1 0.3894 0.0629 0.2837 0.534
## 524 18 1 0.3678 0.0630 0.2628 0.515
## 550 15 1 0.3433 0.0634 0.2390 0.493
## 641 11 1 0.3121 0.0649 0.2076 0.469
## 654 10 1 0.2808 0.0655 0.1778 0.443
## 687 9 1 0.2496 0.0652 0.1496 0.417
## 705 8 1 0.2184 0.0641 0.1229 0.388
## 728 7 1 0.1872 0.0621 0.0978 0.359
## 731 6 1 0.1560 0.0590 0.0743 0.328
## 735 5 1 0.1248 0.0549 0.0527 0.295
## 765 3 1 0.0832 0.0499 0.0257 0.270The summary(fit) tells us how the survival probabilities
change over time for each male and female. Lets use our Kaplan-Meier
survival curve from Challenge 2 to visual the
summary.
We can see that the female survival curve in the lung
dataset have a higher survival probability as time progresses compared
to the male. This suggests that females tend to live longer than males
in the study. However, how do we know this difference is significant? We
will perform our log-rank test using
survdiff() function from the {survival} to
compare the survival curves of females and males
## Call:
## survdiff(formula = Surv(time, status) ~ sex, data = lung)
##
## N Observed Expected (O-E)^2/E (O-E)^2/V
## sex=Male 138 112 91.6 4.55 10.3
## sex=Female 90 53 73.4 5.68 10.3
##
## Chisq= 10.3 on 1 degrees of freedom, p= 0.001We reject the null hypothesis because the p-value is less than 0.05
significance level (p = 0.001). There is sufficient enough evidence to
support that there is a statistically significant difference in survival
times between males and females in the lung dataset.
Next, let’s try to to fit a Cox Proportional model using Karnofsky performance score rated by physicians (ph.karno) as our predictor.
How do the levels of performance rated by physicians compare to survival rate?
First we would have to factor ph.karno into different levels (Low, Medium, High) to compare it to the survival rates. Then, we perform our Cox Proportional model:
# Splitting the ph.Karno into different groups
lung$karno_group <- cut(lung$ph.karno, breaks = c(0, 50, 75, 100), labels = c("Low", "Medium", "High"))
# Cox Model with time-varying effect
cox_m2 <- coxph(Surv(time, status) ~ lung$karno_group, data = lung)
# Check the proportional hazards assumption
cox.zph(cox_m2)## chisq df p
## lung$karno_group 6.3 2 0.043
## GLOBAL 6.3 2 0.043We see that we violate the proportional hazard assumptions because our p-value is less than the 0.05.
So what happens if we violate the proportional hazards assumption?
When we violate the proportion hazard assumption, it means the relationship between a covariate and the hazard rate is not constant over time. So the effect of that variable on survival changes as time progresses.
The Cox Proportional Hazard model assumes that hazard ratios between groups are proportional and do not change over time. If this assumption is violated, the model may produce biased or misleading results.
A common solution is to include time-varying covariates like we learned in challenge 3 to help us model the effects changed over time.
In the lung dataset, a time-varying covariate would be weight loss (wt.loss) which we can use to model with the variable ph.karno (since this alone violate the assumptions).
# Cox Proportional Model
cox_m3 <- coxph(Surv(time, status) ~ karno_group + wt.loss, data = lung)
# Checking assumptions
cox.zph(cox_m3)## chisq df p
## karno_group 5.380 2 0.068
## wt.loss 0.148 1 0.700
## GLOBAL 5.398 3 0.145After adding the time-varying co-variate of weight loss in the last 6 months, we see that the karno_group no longer violates the assumptions of proportional hazard model. However, because karno_group alone violates the proportional hazard assumptions we cannot perform a log-rank test. We would have to use more complex test such as a stratified or weighted log-rank test.
Challenge 5:
Visualizing Competing Risks with CRR
In survival analysis, when we have multiple potential causes of failure (like different types of deaths in our case), we use competing risks models. These models help us estimate the probability of an event happening while considering the influence of other competing events.
CRR focuses on the cause-specific hazard: It models the effect of covariates (like sex) on the risk of death due to lung cancer while considering the competing risk of death due to other causes.
Instead of estimating a single survival curve like we do with CoxPH, the CRR approach gives us Cumulative Incidence Functions (CIF), which represent the probability of experiencing a specific event over time, given the presence of competing risks.
In this challenge, we’ll simulate competing risks using the weight loss variable as an indicator for increased risk of death from causes other than cancer. This will give us a more realistic understanding of survival curves and competing risks.
We’ll continue using the lung dataset and compare survival curves for sex, just like in Challenge 4, but this time we’ll simulate a competing event based on weight loss.
Step 1: We will begin loading our necessary packages:
library(cmprsk) # For competing risks regression
library(dplyr) # For data wrangling
library(ggplot2) # For visualizationStep 2: We will prepare the Lung dataset. Make sure the sex variable is treated as a factor (which it should be already, but just to be safe, we’ll do it here).
## 'data.frame': 228 obs. of 11 variables:
## $ inst : num 3 3 3 5 1 12 7 11 1 7 ...
## $ time : num 306 455 1010 210 883 ...
## $ status : num 2 2 1 2 2 1 2 2 2 2 ...
## $ age : num 74 68 56 57 60 74 68 71 53 61 ...
## $ sex : Factor w/ 2 levels "Male","Female": 1 1 1 1 1 1 2 2 1 1 ...
## $ ph.ecog : num 1 0 0 1 0 1 2 2 1 2 ...
## $ ph.karno : num 90 90 90 90 100 50 70 60 70 70 ...
## $ pat.karno : num 100 90 90 60 90 80 60 80 80 70 ...
## $ meal.cal : num 1175 1225 NA 1150 NA ...
## $ wt.loss : num NA 15 15 11 0 0 10 1 16 34 ...
## $ karno_group: Factor w/ 3 levels "Low","Medium",..: 3 3 3 3 3 1 2 2 2 2 ...## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -24.000 0.000 7.000 9.832 15.750 68.000 14Step 3: We will simulate competing risks based on weight loss
We’ll create a competing risks variable (called cr_status) based on weight loss. The idea is that significant weight loss may be an indicator of more severe health decline, increasing the likelihood of death from other causes like cardiovascular issues or infection.
For this challenge, we’ll assume that wt.loss > 5 kg correlates with a higher risk of death from other causes. We’ll simulate a second event (competing risk) for patients who meet this threshold.
So… Let’s imagine that we have a group of lung cancer patients, and we notice that those who lose more than 5 kg of weight over the course of their illness are at a significantly higher risk of death from complications like infections or heart disease. This competing risk could potentially bias our CoxPH model, which we’ll compare against the CRR model.
This is how it would like in our code:
# Simulate a competing risk based on weight loss (wt.loss > 5 kg means a higher risk of death from other causes)
lung$cr_status <- ifelse(lung$wt.loss > 5,
sample(c(1, 2), size = nrow(lung), replace = TRUE, prob = c(0.7, 0.3)),
0)
# Check the distribution of the new competing risk status
table(lung$cr_status)##
## 0 1 2
## 101 64 49Here, we:
Assign 1 for death from cancer (event of interest).
Assign 2 for death from another cause (competing event).
Assign 0 for censored data (patients still alive or lost to follow-up).
Step 4: Fitting a Competing Risks Regression (CRR) Model
Now, we’ll fit the CRR model (Fine and Gray method) using the newly created competing risk variable (cr_status). This model explicitly accounts for the competing risk and helps us understand how survival probabilities change when competing risks are considered.
# Fit a Competing Risks Regression model using Fine and Gray's method
crr_model <- with(lung, crr(ftime = time, fstatus = cr_status, cov1 = model.matrix(~ sex)[, -1]))## 14 cases omitted due to missing values## Competing Risks Regression
##
## Call:
## crr(ftime = time, fstatus = cr_status, cov1 = model.matrix(~sex)[,
## -1])
##
## coef exp(coef) se(coef) z p-value
## model.matrix(~sex)[, -1]1 -0.312 0.732 0.252 -1.23 0.22
##
## exp(coef) exp(-coef) 2.5% 97.5%
## model.matrix(~sex)[, -1]1 0.732 1.37 0.447 1.2
##
## Num. cases = 214 (14 cases omitted due to missing values)
## Pseudo Log-likelihood = -302
## Pseudo likelihood ratio test = 1.44 on 1 df,# Plot the cumulative incidence curves (CRR model)
cif <- with(lung, cuminc(ftime = time, fstatus = cr_status, group = sex))## 14 cases omitted due to missing values# Plot the cumulative incidence curves
plot(cif, xlab = "Time (Days)", ylab = "Cumulative Incidence",
main = "CRR Model: Cumulative Incidence by Sex",
col = c("blue", "red"))
legend("bottomright", legend = names(cif), col = c("blue", "red"), lty = 1)This will generate cumulative incidence functions (CIF), which show the probability of death from cancer (the event of interest) and death from other causes (competing event) over time, adjusted for sex.
So again, what have we learned of CRR modeling?
The CRR model explicitly accounts for competing risks, giving a more realistic picture of survival probabilities when studying specific causes of death.
Conclusion:
Survival analysis is a powerful tool for studying the timing of
events, especially when dealing with incomplete or censored data.
In this module, you’ve learned how to apply key survival analysis
techniques in R, including the Kaplan-Meier estimator and Cox
proportional hazards model. These methods are essential for analyzing
real-world data where timing matters.
By the end, all of you should feel more confident working with time-to-event data, interpreting survival curves, comparing groups, and understanding how risk changes over time!
References:
Bryan Lau, Stephen R. Cole, Stephen J. Gange, Competing Risk Regression Models for Epidemiologic Data, American Journal of Epidemiology, Volume 170, Issue 2, 15 July 2009, Pages 244–256, https://doi.org/10.1093/aje/kwp107
Camilleri, L. (2019, March 24). History of survival analysis. The Sunday Times of Malta, p. 53. Retrieved from https://www.um.edu.mt/library/oar/handle/123456789/55748
Fox J, Weisberg S. (2001). Cox Proportional Hazard Regression for Survival Data. https://www.researchgate.net/publication/239487024_Cox_Proportional_Hazard_Regression_for_Survival_Data
Goel MK, Khanna P, Kishore J. Understanding survival analysis: Kaplan-Meier estimate. Int J Ayurveda Res. 2010 Oct;1(4):274-8. doi: 10.4103/0974-7788.76794. PMID: 21455458
Mustafa A. (2024). Getting Started with the Cox Proportional Hazards Model: A Hands-On Guide in R. Medium. Retrieved from https://medium.com/@akif.iips/getting-started-with-the-cox-proportional-hazards-model-a-hands-on-guide-in-r-291f4e85589a
Rich, J. T., Neely, J. G., Paniello, R. C., Voelker, C. C. J., Nussenbaum, B., & Wang, E. W. (2010). A practical guide to understanding Kaplan‐Meier curves. Otolaryngology–Head and Neck Surgery, 143(3), 331–336. https://doi.org/10.1016/j.otohns.2010.05.007
Therneau, T., Crowson, C., & Atkinson, E. (2024). Using Time Dependent Covariates and Time Dependent Coefficients in the Cox Model.
Vianda S. Stel, Friedo W. Dekker, Giovanni Tripepi, Carmine Zoccali, Kitty J. Jager; Survival Analysis I: The Kaplan-Meier Method. Nephron Clinical Practice 1 August 2011
Zhang Z, Cortese G, Combescure C, Marshall R, Lee M, Lim HJ, Haller B; written on behalf of AME Big-Data Clinical Trial Collaborative Group. Overview of model validation for survival regression model with competing risks using melanoma study data. Ann Transl Med. 2018 Aug;6(16):325. doi: 10.21037/atm.2018.07.38. PMID: 30364028; PMCID: PMC6186983.
Zabor E. C. (2025). Survival Analysis in R. https://www.emilyzabor.com/survival-analysis-in-r.html